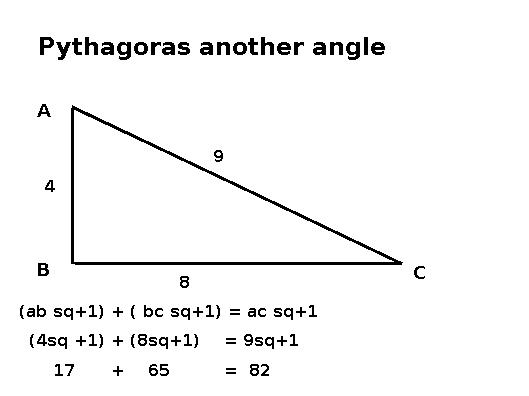
|
One
so-called 'irrational number' that I have not yet
explained, Phi 1.618..., relates to what is known
as "The Divine Proportion". This contribution also
comes from the Pythagorean school. This a
window that is pleasing to the eye and which has a
relationship in which the
width to the length of the window is 8
to 13. This relationship
is derived from the Pythagorean theorem for
a rectangle as shown in the sketch below.
 The
construction
of
the Golden Rectangle is done by first
constructing a square, and then by projecting the
diagonal of half the square, onto the base as
shown in the sketch below.
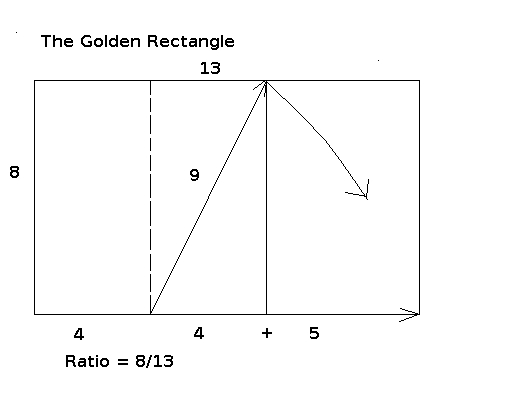 The Golden section is obtained by projecting the side of the Golden rectangle onto the base. The following dimensions are then established: The whole ( base ) = 13 units The long section = 8 units (also referred to as the mean) The short section = 5 units The ratio of the long section to the whole is 8/13 The ratio of the short section to the long section is 5/8 The least is to the mean as the mean is to the greatest. 5/8 is as 8/13 The equation that satisfies these ratios is: 64=65 The
rectangle
is
composed of 64 small rectangles.
It will be irrational to say that the the rectangle continues to diminish indefinitely. The rectangle is finite and is made up of 64 rectangles. The idea that there is an infinite number of rectangles is a fallacy. The sequence of depletion of the rectangles is as follows: 32,16,8,4,2,1,1 for a total of 64 rectangles. " The law of the LORD is perfect, converting the soul: the testimony of the LORD is sure, making wise the simple." 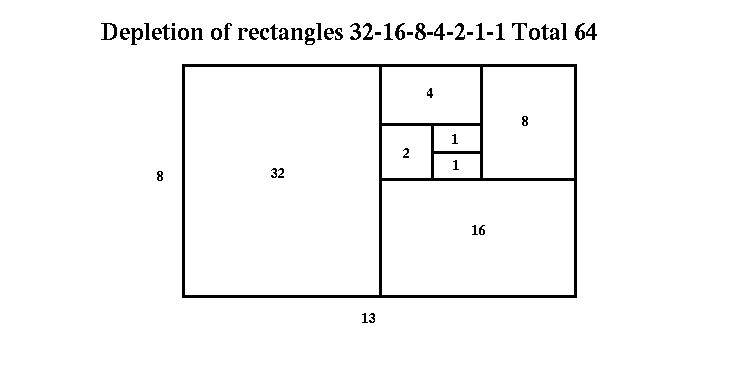 Divine Proportion |