(Pythagoras revisited)
" The lord of that servant will come in a day
when he looketh not for him,
and at an hour when he is not aware,
and will cut him in sunder,
and will appoint him his portion with the unbelievers."
|
The purpose of
this message is to show the different proportions
between the sides, and diagonals, of squares and
rectangles. Proportion is the harmonious relation of
parts to each other, or to the whole. In addition we
will verify that a valid equation is always sequential,
as well as the validity of the revised Pythagorean
theorem.
Therefore
BD
will also be 24 unitsDraw a diagram ABCDEF as shown so that: a) ABEF is a square with sides 17 units in length. b) AE and BF are diagonal lines crossing at G. c) FE is extended to D so that FE=ED=17 units. d) EC is drawn perpendicular to BD so that BC=CD. e) All six triangles are congruent.(One 90 Degree and two 45 degree angles, or 2 equal sides each) Therefore we know that: CD/ED=ED/BD=BD/FD -------(1) (The basic law of geometric proportion) 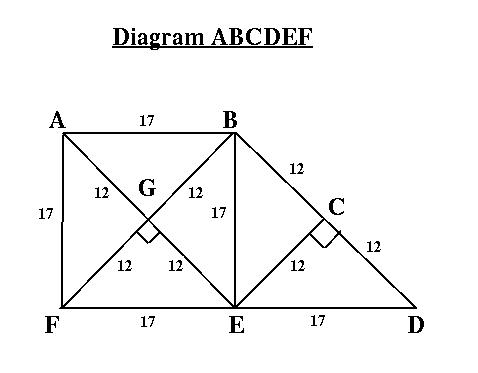 Now assume that the diagonal AE and BF = 24 units. and BC=CD=EC=AG=GE=BG=GF=12 units. Substitute values for ---------(1) 12/17= 17/24 = 24/34 ------------------(2) therefore 12/17 = 17/24 (valid proportion) ------> cross multiply 288 = 289 (valid equation) ------> From the diagram it is also clear that; surface area ABEF = (2) x (surface area BCEG) (CD sq+1) + (CE sq+1) = (ED sq+ 1) (The Pythagorean Theorem) -----------> The assumption that the diagonal AE = 24 units has been proven to be correct. Addendum The surface area of BCEG is 12sq+1 = 145 units--(1) The surface area of ABEF is 17sq+1 = 290 units--(2) The surface area of which BD is a side = 580 units--(3) The surface area of which FD is a side = 1160 units-(4) The overlap for (1)&(2) is one (1x1) The overlap for (3)&(4) is four (2x2) The overlap is determined from the base triangle. (12 12 17) It is then transferred to the secondary triangles. (17 17 24) and (24 24 34) ---------------------> |