Believers Information Network




The Pythagorean Theorem
(Making it real)

" Rest satisfied with doing well,
 and leave others to talk of you as they will."

Pythagoras


" (iv) The discovery of irrationals. This is certainly attributed to the Pythagoreans but it does seem unlikely to have been due to Pythagoras himself  This went against Pythagoras's philosophy the all things are numbers, since by a number he meant the ratio of two whole numbers. However, because of his belief that all things are numbers it would be a natural task to try to prove that the hypotenuse of an isosceles right angled triangle had a length corresponding to a number."
School of Mathematics and Statistics University of St Andrews, Scotland

Introduction

The purpose of this short message is to make it clear that the side and the diagonal of a square are commensurable.This means that we can use a square to show that:

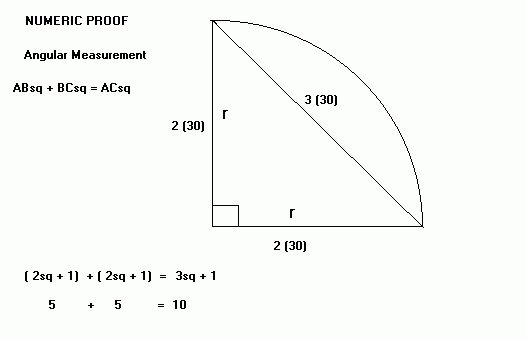
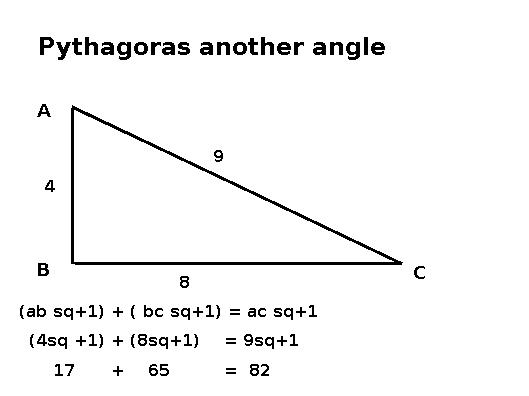
AB sq + BC sq = AC sq (equation)

There is no need to skew a triangle in order to put numerical values to the three sides. More important is that it shows there is no need for irrational numbers. The length of the side of a square is 12/17. Rational numbers can fill in all the gaps fabricated by irrational man.

The diagrams are self explanatory, the addition of one after each side is squared, is to give substance to the surface area. Without this addition the surface areas will only be two dimensional, a meaningless abstraction, a superficial area.
The revised theorem is:

(ABsq+1) + (BCsq+1) // (ACsq+1)

Without any practical value, mathematics becomes a senseless exercise in futility.



Note: The slanted surface area is greater than the superficial area, however, when  the  surface area  is  made even, by means of a wedge, it becomes  equal  to the superficial area. The difference is that it now has substance(depth), and is known as a surface area.




Another Perspective
The Pythagorean Theorem is also valid should we draw a rectangle instead of a square. Another contribution that came from the Pythagorean school is the so called "golden rectangle" which is derived from this rectangle. The structure of the famous Parthenon was build using the so called "divine proportion".

Proportion

Let us see how Pythagoras relates to proportion.
I quote  Plato(Timaeus),  a follower of  Pythagoras:

"It is impossible to join two things in a beautiful manner without a third being present, for a bond must exist to unite them, and this is best achieved by a proportion. For , if of three magnitudes the mean is to the least as the greatest to the mean, and , conversely, the least is to the mean as the mean to the greatest- then is the  last the first and the mean, and the mean the first and the last.  Thus are all by necessity the same, and since they are the same, they are but one."

Now let us examine the sketch.


 

 Least / Mean  =  Mean / Greatest

            s-x / x   = x / s
               x sq   = s ( s-x )
               x sq   = s sq - sx
x sq + sx - s sq // 1 (They are but one  " Plato ")
    Substituting values from Pythagoras and we have:
 5sq + 5*8 - 8sq // 1
  25  + 40 - 64    // 1  -------------->

Also 5/8 = 8/13   is  64=65 (a valid equation.)


ADDENDUM-82016

I MAKE THE DISTINCTION BETWEEN AN EQUATION AND
A SUMMATION.

MY SYMBOL FOR AN EQUATION   " = "
MY SYMBOL OF A SUMMATION     " // "

AN  EQUATION IS SEQUENTIAL 
a = a + 1 = b
A SUMMATION REPRESENTS " IN  PLACE  OF "(TAUTOLOGY)
3 + 4  //  7

a sq + b sq = c sq (equation)
12 sq + 12 sq = 17 sq     (Pythagoras)
144 + 144  = 289 (a valid equation)
(12sq + 1) + ( 12sq + 1) // 17sq + 1 (Pythagoras theorem)
145 + 145  //  290 (Summation)

a/b = b/c  ( PROPORTION)
12/17 = 17/24  (Pythagoras)
288 = 289  (VALID EQUATION)
THEREFORE C // 2A // 24

ALL VALID NUMBERS ARE QUANTITATIVE.
THERE IS ONLY ONE WHOLE NUMBER 1(ONE).
ALL OTHER NUMBERS ARE RATIONAL NUMBERS.
A  RATIONAL  NUMBER  HAS  TWO  PARTS,
A NUMERATOR(PART)  AND  A  DENOMINATOR(WHOLE).
IN THE NUMBERING SYSTEM RATIONAL NUMBERS REPRESENT  RELATIONSHIPS(RATIOS)

ZERO IS NOT A NUMBER,
IT  IS NON  QUANTITATIVE(IRRATIONAL)
ALL THE SO CALLED  ' WHOLE NUMBERS(INTEGERS 2.3.4..) '
ARE IRRATIONAL, THE PART IS LARGER THAN THE WHOLE, WITH THE EXCEPTION OF ONE, WHICH IS THE ONE AND  ONLY  WHOLE NUMBER.
  
 

The Legacy of Pythagoras - Part One





The Legacy of Pythagoras - Part Two