Pythagoras
(The 3-4-5
fallacy) " Let no man deceive himself.
If any man amongst you seemeth to be wise
in this world, let him become a fool,
that he may be wise. "
| The Pythagorean theorem states
that the sum of the surface areas generated by the
sides of a right triangle, is equal to the surface
area generated by the the hypotenuse. Traditionally the example used to illustrate the Pythagorean theorem is the 3- 4- 5 diagram. This is a fallacy, and the purpose of this message it show why it is a fallacy. The formula for the Pythagorean theorem can be stated as follows: (a sq + 1) + ( b sq +1) = (c sq + 1) The incorrect formula omits the +1 for each value. It simply states that: a sq + b sq = c sq. The addition of one for each value is necessary in order to convert the area, to a surface area. In reality there can be no area without a surface. The "one" that is added, makes the area real, it adds the third dimension of substance, to the formula. From a practical point of view it can be seen as one square area being overlapped when we multiply length by width. The 3-4-5 formula is an approximation and was apparently used by ancient builders in order to make sure that everything was 'square'. If we apply the revised formula then we have: (3sq + 1) + (4sq + 1) = 5sq + 1 10 + 17 = 25 + 1 27 = 26 (not equal to) From the calculation we can see that the hypotenuse is to short. The sketch below shows how the 3-4-5 formula distorts the right angle, making it acute(less than 90 degrees). 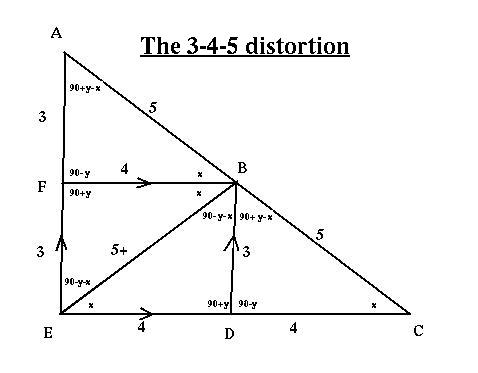 Notice that the only linear deviation, is the length EB, which is extended beyond 5 units in order to accommodate the distortion caused by the faulty formula. Needless to say all the angles are distorted. The values for x and y are : x = 44 3/4 degrees y = 1/4 degree 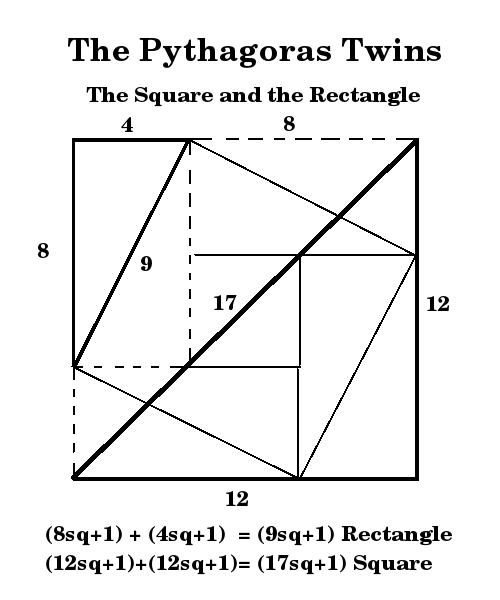 The actual values for surface areas are shown above. 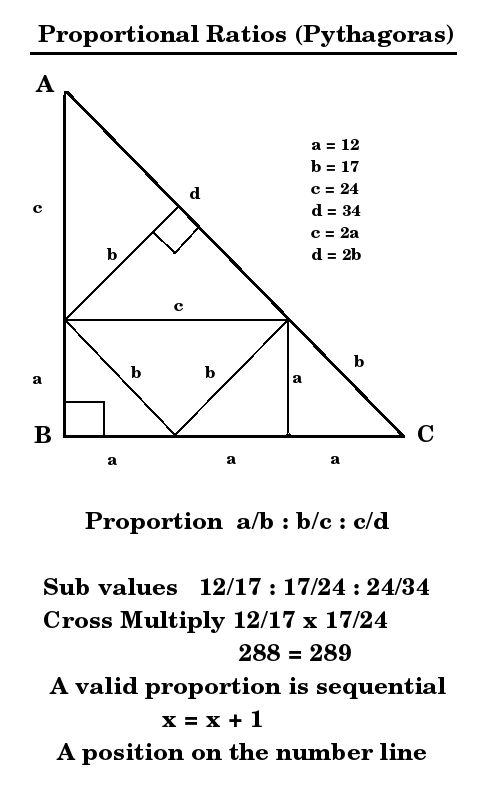 |