Pythagoras
Meets Hippocrates
We now examine the the geometric implications of Py.
We redefine Py, based on our previous definition where we used circumferences:
Py is the the relationship(ratio) of the area of a circle, to the area of a
square, with the diameter of the circle being equal to the side of the square.
Referring to our diagram below:
Py(11/14) will be:
Area of circle O(11) with diameter HD / Area square ACEGA(14) with side HD.
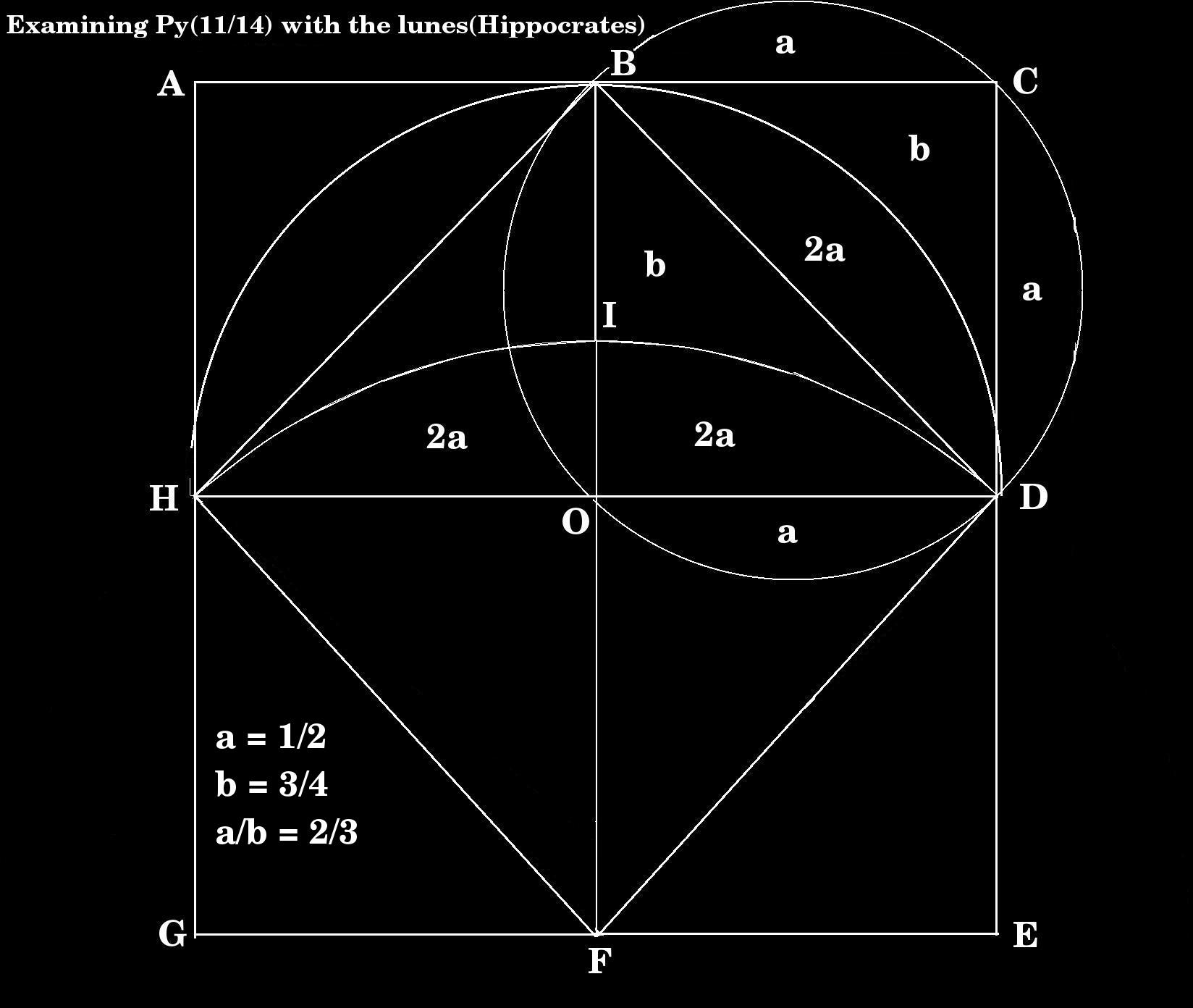
Referring to the diagram the following:
Consider the the square ACEGA and the Circle O.
1. Allocate surface areas a and b to lune BCD.
2. Surface area bow HID is 4a.(Pythagoras- BC=a, BD= 2a, HD =4a)
3. Area lune BCD is equal to area triangle BOD(Hippocrates)
4. Therefore area BID is equal to area b.
5. Consider area square BCDO: 2b + 4a
6. Area square ACEG = 4 x (4a + 2b) = 16a + 8b --------- 1
7. Area circle segment BOD = 4a + b
8. Area circle O = 4 x (4a + b) = 16a + 4b ----------2
We are now able to establish rational values for a and b.
9. Substituting for square 16a + 8b = 14 ------- 1
10. and for circle 16a + 4b = 11 ------- 2
11. 1-2 4b = 3
12. b = 3/4 ----------->
13. substituting b in --1 16a + 6 = 14
14. 16a = 8
15. a = 1/2 ----------->
By substituting these values in our diagram we find no conflicts.
Area of square ACEGA = 14
Area of square BDFH = 7
Area of circle O = 11
Py 11/14
We have managed to unite the square and the circle into
one harmonious rational diagram with no conflicts.