Pi
and

Squaring the Circle

" O Timothy, keep that which is committed to thy trust,
avoiding profane and vain babblings,
and oppositions of science falsely so called: "

L. Kronecker

Pi and The Circle

Pi Before we show the reader how to square a circle, using only a straight edge and compass, we need to examine  some characteristics of Pi, as well as a circle. Pi is supposed to be a symbol that expresses the relationship(ratio) between the diameter and the circumference of a circle. In the present system, Pi is the irrational number 3.14159.... This number is a fabrication of the irrational mindset, and can be explained as follows: We know that the relationship between the radius(r) of a circle, and it's circumference(c), is 1:6. We also know that the diameter of a circle is twice the radius. It therefore follows that the relationship between the diameter and the circumference of any circle is 2:6 or 1:3. This is also confirmed in  I Kings 7:23 of the old testament in the bible. What the irrational mindset has done is to express the straight line diameter of a circle, with the curved line of it's circumference. This is like expressing oranges(d), as a part of apples(c). No surprise that the result is irrational. Should we express the ratios of the straight lines, as well as the ratios of the curved lines, we will see that they are both 1:3. The Circle When we work within the parameters of a circle, we need to establish a constant factor which will enable us to convert a straight line to a curved line, and vise versa. This will then enable is to convert straight, as well as curved lines of segments. The relationship(ratio) between the chord and the arc of  a radius segment is the constant: (k) = 21/22 (see I Kings 7:21&22). This means that if we have a chord(r) with a length of  21 units, the arc will measure 22 units in a straight line(laid flat). The radius of a circle can geometrically be shown as a straight line, or as a curved line, both representing 60 degrees. (This means a radian should be 60 degrees, and not some  fabricated value derived from irrational Pi - It does not make sense to separate the chord from the arc, they are one segment ). Now we are able to establish a relationship between the straight line (diameter), and the converted curved line (circumference) of a circle. In other word the curved(c) line, laid flat. We measure in units of straight lines(21), or curved lines(22). The diameter will measure 2x21=42 units and the circumference will measure 6x22=132 units. The ratio(relationship) between the straight line diameter and the converted curved line circumference will be 42:132 or 7/22, a rational number. It is important to note that this is not the relationship between the diameter and the circumference of a circle. The relationship(Pi) remains as 42:126, that is 1:3. The  ratio of 7:22 is a rational conversion ratio, as opposed to an irrational relationship. 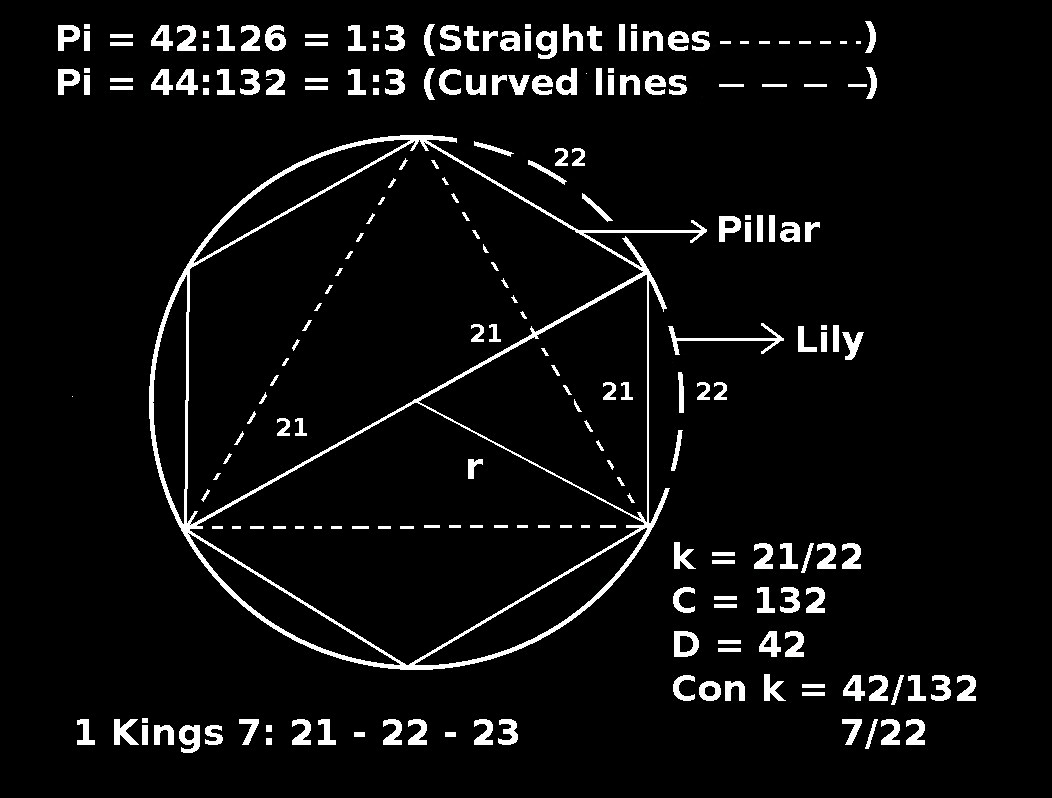Py We are  now in a position to establish a constant that will enable us to calculate the circumferences, areas and volumes of circles and spheres. We will call this constant  Py. Py is a rational number and is derived as follows: We know that the straight line relationship of the diameter of a circle and the straight line circumference  of a circle is 7 to 22.  This means that the ratio of  the straight line, of one side side of a square, to the diameter of the circle is  22/4 = 5 1/2 to 7, or more conveniently stated as 11 to 14.  This then is the new value for Pi, which we will call Py, in order to make the distinction between the irrational Pi, and the rational Py. Let us now see how we can apply this new Py to our practical formulas:        Circles                    Old                     New Circumference       d    x   Pi                   4 d   x    Py Surface Area         r  sq  x   Pi            ( d sq   x   Py) + 1 Spheres                  Old                     New Surface area       4  x  r sq   x  Pi         (4  x   d sq   x  Py)  Volume             4/3  x  r 3rd  x  Pi      2/3  x   d 3rd  x  Py When we apply the new value Py,  the results differs slightly from the old values  for  Pi, results are expressed as real values, not approximations.  Squaring the circle Problem: Given any circle, to construct a square with the same surface area as the circle, using only a straight edge and compass. Solution: 1. Draw any circle with diameter AOB. (This is the circle we will square) 2. Sub divide AB into 14 equal parts. 3. From the centre of the circle mark off  6 parts in both directions as line COD. (12 parts). 4. From C draw a line  perpindular to the diameter. 5. Mark off  3 parts at E on the perpendicular line and connect  DE. 6. Draw square DEFG. Square DEFG has the same surface area as circle AOB. 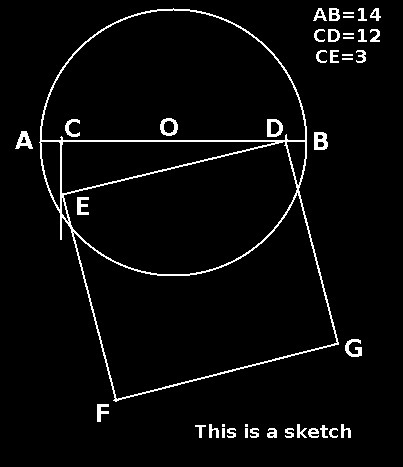Confirmation: Apply the Pythagoras theorem to calculate the area of  DEFG. (CD sq + 1) + (CE sq +1) = ED sq +1       (144 +1)  + ( 9 + 1) = (154 + 1) ------------> Apply Py to calculate the area of circle AOB. (D Sq  x Py) + 1 (14 sq  x 11/14) + 1 (154 + 1)  ---------------> Now that all three problems of antiquity are resolved it is time to bring in the harvest and to celebrate. Note: Using  Pi (irrational) for calculations results in approximations. Another great discovery, Pythagoras meets Hippocrates. Pi and squaring the circle Part 1 Pi and squaring the circle Part 2 Pi and squaring the circle Part 3